what is 3 to the power of 2
(These buttons explained below)
Question Corner and Discussion Surface area
Why is e^(pi i) = -i?
Asked by Brad Peterson, student, Roy Loftier on Jan 29, 1997:I was watching an episode of The Simpsons the other day, the one where Homer gets sucked into the third dimension, and in this three-D world, there was an equation that saidWe'd be glad to explain; that's exactly what this area is here for.. Then I put it into the calculator and it worked, but I take no idea why, because e to any power isnt supposed to be a negative number, and I thought pi was in no way related to eastward.
If you could explain the process, it would salvage lots of fourth dimension pondering and plugging e, pi, and i into the calculator in random means to figure out whats going on.
The first question to ask, though, is not "why does 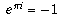", just rather, "what does 
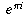even mean?" In other words, what does it mean to raise a number to an imaginary power?
Once that question is answered, it will be much more clear why 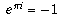. It turns out that 
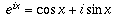for all x, a fact which is known as de Moivre's formula, and illustrates how closely related the exponential function is to the trigonometric functions. From this formula, it follows immediately that 
.
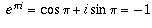So at present, the question is, why is 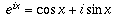the "correct" thing to define what e raised to an imaginary ability means?
Raising a number to an imaginary power makes no sense based on the original definition of exponentiation y'all learned, where 
means "a multiplied past itself b times." That definition only makes sense when b is a positive integer. After all, what would it mean to multiply something by itself i times??
Of course, the original definition doesn't fifty-fifty brand sense for fractions and negative numbers. Y'all should have learned how to extend the definition to include fractions. For example, since 1/three is that number which, when multiplied by 3, gives you ane, it makes sense to ascertain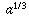 
to be that number which, if you raise it to the power of iii, would give you 
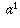(i.eastward., a); in other words, 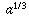is defined to be the cube root of a. Similarly, you learned how to extend the definition to negative exponents by 
.
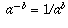Simply none of these considerations requite any clue as to what raising a number to a circuitous ability should mean. Instead, we need to limited exponentiation, or its backdrop, in some way that can be extended to complex powers.
The first fashion to do this is to use the fact that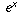 
happens to exist equal to the infinite sum
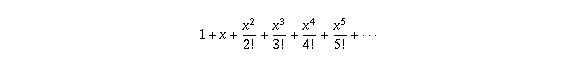
(where n! means n factorial, the product of the numbers 1,ii,. . . ,n).
The reason why this is then depends on the theory of Taylor series from calculus, which would have too long to describe here. You lot volition encounter information technology in a calculus class at some point, if you lot haven't already.
Now, this infinite sum makes perfectly good sense even for imaginary numbers. By plugging in ix in place of x, you lot go
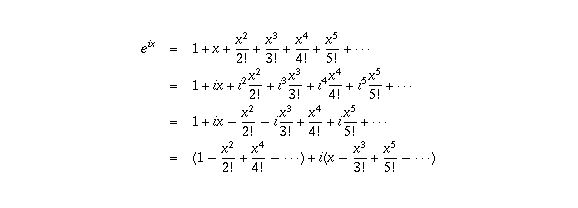
Now it turns out that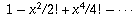 
is the infinite sum for cos x, while 
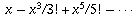is the infinite sum for sin x (again by the theory of Taylor series). Therefore, .
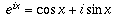Now, this may exist a little unsatisfying to y'all since I haven't explained why 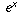, cos x, and sin ten equal those iii different infinite sums. I can't exercise and so without assuming some calculus groundwork that you may not have.
Nonetheless, hither'southward some other way of understanding why 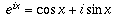. It too involves some calculus, but I can describe the calculus involved more than hands.
Associated to many functions f(ten) is another office f'(x), called the derivative of f(x). It measures how rapidly f(x) is irresolute at the value x.
If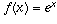 
, f(x) may represent, for case, an exponentially growing population. The rate of change of such a population (the number of births per day, for example) is directly proportional to the current size of the population; that is, f'(x) is a constant times f(x). When 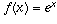, that constant is exactly ane (that's the holding which defines the number e). More than mostly, if 
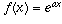, so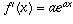 
.
What well-nigh the trigonometric functions? Well, if f(ten) = sin x, then f'(ten) = cos x, and if f(10) = cos x, so f'(x) = - sin 10.
If you call up virtually it for a minute, these equations are very reasonable. Outset of all, when x=0, sin x equals zilch but increases as x increases; in fact, the slope of the graph of y = sin x at the point (0,0) is 1, which is some other way of saying that the rate of increase in that location is 1, and so f'(0) = 1.
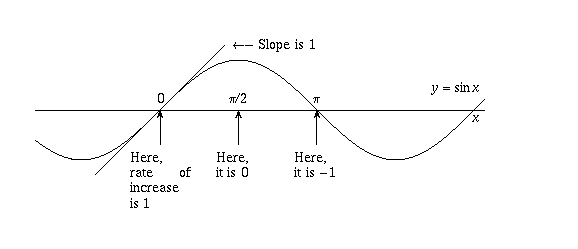
But then, equally 10 increases to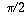 
, the rate of increase drops off and eventually sin 10 stops increasing altogether and starts decreasing. In other words, f'(x) drops to zero when 
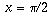, and becomes -ane by the fourth dimension x reaches pi (see the moving-picture show).
Therefore, f'(x) is a function which starts at one when x=0, decreases to 0 when 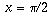, drops to -1 when 
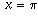, rises back to 0 when 
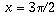, and so on. This is precisely what the cosine part does, so it should be no surprise that f'(ten) = cos 10. Similar reasoning shows why it is reasonable that, when f(x)=cos x, f'(10)=-sin x. The exact proofs of these facts you lot will encounter in a calculus form.
Now, keeping those facts in mind, what should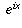 
exist? If we write it in terms of existent and imaginary parts thousand(x) + i h(ten), what should the functions g(ten) and h(x) be?
The fundamental is to take the derivative. Information technology is just reasonable to ascertain 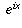in such a fashion that information technology all the same has the same properties as mentioned in a higher place, namely, the derivative of 
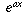should still equal 
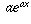. Therefore, if 
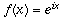, we should have
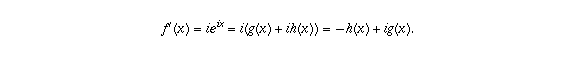
But f'(x) should likewise equal g'(x) + i h'(x), so we are looking for a pair of functions yard and h for which h' = g and g' = -h. This is exactly the same interrelationship that the sine and cosine functions accept, equally we saw above. It also turns out that these two equations, together with the conditions g(0)=one and h(0)=0 that arise from the fact that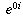 
needs to equal ane, uniquely determine the functions grand and h.
It follows from all this that thou must be the cosine office and h must exist the sine function. That is why .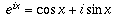
This office of the site maintained past (No Current Maintainers)
Terminal updated: April 19, 1999
Original Web Site Creator / Mathematical Content Developer: Philip Spencer
Electric current Network Coordinator and Contact Person: Joel Chan - mathnet@math.toronto.edu
Navigation Panel:
Go to University of Toronto Mathematics Network Home Folio
Source: https://www.math.toronto.edu/mathnet/questionCorner/epii.html
Post a Comment for "what is 3 to the power of 2"